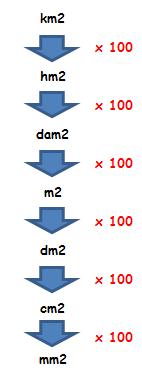
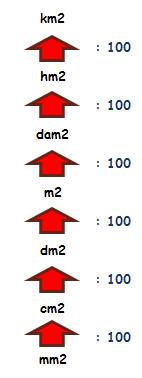
Para pasar de unidades menores a unidades mayores hay que dividir por 100 por cada nivel que subamos:
Por ejemplo:
Para pasar de m2 a hm2 hay que subir 2 niveles por lo que tenemos que dividir : 100 : 100 = : 10.000
Para pasar de cm2 a dam2 hay que subir 3 niveles por lo que tenemos que dividir : 100 : 100 : 100 = : 1.000.000
Veamos algunos ejemplos numéricos:
¿Cuantos m2 son 60.000 cm2? 60.000 : 10.000 = 6 m2
¿Cuantos km2 son 8.000.000 m2? 8.000.000 : 1.000.000 = 8 km2
¿Cuantos dm2 son 75.000 mm2? 75.000 : 10.000 = 7,5 dm2
Ejercicio
1. Calcula las siguientes conversiones:
| 1) | 7 m2 = mm2 | |
| 2) | 8 dm2 = cm2 | |
| 3) | 13 cm2 = mm2 | |
| 4) | 21 m2 = mm2 | |
| 5) | 13 m2 = mm2 | |
| 6) | 21 m2 = dm2 | |
| 7) | 7 dm2 = cm2 | |
| 8) | 8 cm2 = mm2 | |
| 9) | 7 m2 = dm2 | |
| 10) | 15 dm2 = mm2 | |
| 11) | 6 km2 = m2 | |
| 12) | 9 hm2 = dam2 | |
| 13) | 13 dam2 = m2 | |
| 14) | 15 km2 = dam2 | |
| 15) | 18 dam2 = m2 | |
| 16) | 25 km2 = dam2 | |
| 17) | 12 km2 = hm2 | |
| 18) | 11 dam2 = m2 | |
| 19) | 14 km2 = hm2 | |
| 20) | 10 hm2 = m2 | |
| 21) | 8 km2 = dm2 | |
| 22) | 9 dm2 = mm2 | |
| 23) | 11 dam2 = dm2 | |
| 24) | 18 hm2 = dm2 | |
| 25) | 19 m2 = mm2 | |
| 26) | 31 hm2 = mm2 | |
| 27) | 7 dam2 = cm2 | |
| 28) | 9 cm2 = mm2 | |
| 29) | 17 dam2 = cm2 | |
| 30) | 7 km2 = dam2 | |
Corregir Ver Solución Limpiar | ||