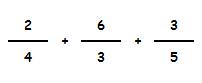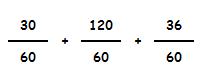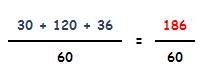Esta semana, dentro de nuestro Proyecto Emocionario, trabajaremos la tensión. Una irritación muy duradera nos lleva a sentir tensión.
domingo, 29 de noviembre de 2020
LA TENSIÓN. EL EMOCIONARIO
JUEGO DE FRACCIONES
Suma y resta de fracciones con diferente denominador
¿Cómo sumar y restar fracciones con diferente denominador?
Lo primero que hay que hacer es buscar un denominador común a todas ellas. Luego sustituir las fracciones originales por fracciones equivalentes con este denominador común.
Pero, ¿cómo se calcula este denominador común?
Una manera sencilla de calcularlo es multiplicar todos los denominadores. El resultado de esta operación es el denominador común.
Hay una forma más correcta de calcularlo a través del mínimo común múltiplo. Pero se trata de una forma más compleja que queda para el Curso gratis de Matemáticas para Segundo de la ESO.
Así que una vez obtenido el denominador común hay que calcular las fracciones equivalentes. Para cada fracción haremos lo siguiente.
- Sustituimos su denominador por el denominador común.
- Calculamos su numerador de la siguiente manera: dividimos el denominador común por el denominador original de cada fracción. El resultado obtenido lo multiplicamos por el numerador original, obteniendo el numerador de la fracción equivalente.
Tranquilo, es más fácil de lo parece. Lo entenderás perfectamente con este ejemplo:
Vamos a hacerlo paso a paso:
1.- Primero calculamos el denominador común: 4 x 3 x 5 = 60
Ahora vamos a calcular el numerador equivalente de cada fracción:
Primera fracción:
Dividimos el denominador común entre su denominador: 60 : 4 =15
Multiplicamos este resultado por su numerador: 15 x 2 = 30
Segunda fracción:
Dividimos el denominador común entre su denominador: 60 : 3 = 20
Multiplicamos este resultado por su numerador: 20 x 6 = 120
Tercera fracción:
Dividimos el denominador común entre su denominador: 60 : 5 =12
Multiplicamos este resultado por su numerador: 12 x 3 = 36
Ya podemos sustituir las fracciones originales por sus fracciones equivalentes:
Para terminar, procedemos a la suma:
¿Ves qué fácil? Sumar y restar fracciones con distinto denominador nunca había sido tan fácil.
Para descubrir si lo has entendido bien, haz estos ejercicios de suma y resta de fracciones y comprueba tu nivel.
Ejercicios de suma y resta de fracciones
Con estos ejercicios de suma y resta de fracciones para primaria podrás practicar estas operaciones y descubrir si has entendido perfectamente cómo se resuelven estos problemas.
Se trata de una tabla interactiva así que podrás ver el resultado al final del ejercicio para ver cuáles has acertado y cuáles no. Además, podrás repetirlo las veces que quieras. Solo tienes que borrar los resultados y volver a empezar.
1. Resuelve las siguientes operaciones:
| 1) | 4/6 + 3/6 + 2/6 = | |
| 2) | 1/3 + 2/3 + 4/3 = | |
| 3) | 4/5 + 5/5 + 3/5 = | |
| 4) | 12/8 - 6/8 - 3/8 = | |
| 5) | 10/2 - 4/2 - 3/2 = | |
| 6) | 12/6 - 6/6 - 3/6 = | |
| 7) | 11/7 + 4/7 - 3/7 = | |
| 8) | 18/4 + 9/4 - 6/4 = | |
| 9) | 9/4 - 5/4 + 3/4 = | |
| 10) | 2/4 + 3/5 + 1/3 = | |
| 11) | 5/2 - 4/5 + 3/6 = | |
| 12) | 6/2 + 3/4 + 5/3 = | |
| 13) | 6/3 - 5/4 - 1/2 = | |
| 14) | 9/3 + 4/3 + 2/3 = | |
| 15) | 5/1 - 7/4 + 5/3 = | |
Corregir Ver Solución Limpiar | ||
SUMAR Y RESTAR FRACCIONES
Para realizar una suma o resta de fracciones deben tener el mismo denominador.
Podemos encontrarnos diferentes casos.
Suma o resta de fracciones con el mismo denominador
Al tener el mismo denominador en las fracciones que vamos a sumar o restar, dejamos el mismo denominador y sumamos o restamos el numerador.
Vamos a ver un ejemplo. Si sumamos 7/10 y 10/10, dejamos 10 como denominador de la fracción resultante y sumamos los numeradores, 7 + 10 = 17. Por lo que el resultado de la fracción sería 17/10.
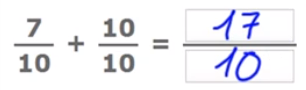
Aquí puedes ver el tutorial de la suma de fracciones con el mismo denominador y practicar ejercicios.
Suma o resta de fracciones con denominadores coprimos (no tienen divisores en común)
Para calcular la suma o resta de este tipo de fracciones tendremos que multiplicar los denominadores para hallar el denominador de la fracción resultante, y para conseguir el numerador tendríamos que multiplicar el numerador de una de las fracciones por el denominador de la otra y viceversa, y posteriormente, sumar o restar el resultado, dependiendo del tipo de operación que tengamos que realizar.
Vamos a poner un ejemplo. Sumemos 11/10 + 2/3.
Los denominadores son 10 y 3, que son diferentes y no tienen divisores en común, por lo que tendremos que multiplicarlos entre ellos. 10 x 3 = 30, por lo que 30 será el denominador de la fracción resultante.
Para calcular el numerador, tendremos que multiplicar 11 x 3 = 33 y 10 x 2 = 20, y sumar los resultados, 33 + 20 = 53, que sería el numerador de la fracción obtenida.
El resultado final de la suma sería: 53/30
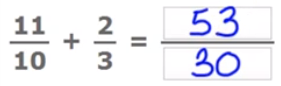
Suma o resta de fracciones con un denominador que es divisor del otro
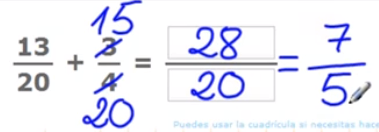
Vamos a ver un ejemplo para que quede más claro. Vamos a sumar 13/20 + 3/4.
Los denominadores de estas fracciones son diferentes pero el 4 es un divisor de 20, podemos multiplicar el 4 por un número para que nos dé 20, es decir, por 5. Multiplicamos tanto el numerador como el denominador de 3/4 por 5 y nos quedaría 15/20 y realizamos la suma de ambas fracciones, que nos daría como resultado 28/20. Pero 28/20 se puede simplificar ya que 28 y 20 son múltiplos de 4, por lo que dividimos numerador y denominador entre 4, teniendo 7/5 como resultado final.
Suma o resta de fracciones utilizando el mínimo común múltiplo (mcm)
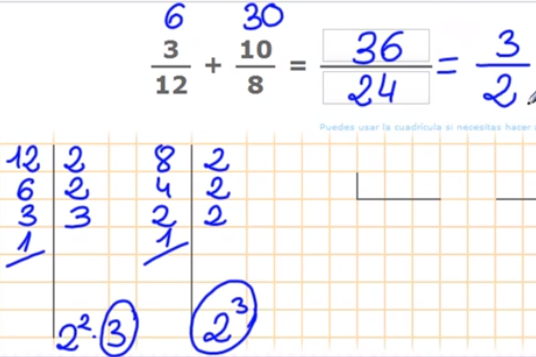
Veamos a continuación un ejemplo. Vamos a sumar 3/12 + 10/8.
12 y 8 son los denominadores de las fracciones a sumar, que son diferentes entre sí y tienen divisores en común, por lo que vamos a descomponer factorialmente los números para saber cuál es el mínimo común múltiplo, como muestra en la imagen que tenemos posteriormente.
12 = 22 x 3 8 = 23
Para calcular el mínimo común múltiplo tenemos que coger los divisores comunes y no comunes elevados al mayor exponente. 23 x 3 = 24
Por lo tanto, el denominador común es 24.
Ahora, para calcular el numerador de cada una de las fracciones que vamos a sumar, dividimos el mínimo común múltiplo calculado entre el denominador, y el resultado lo multiplicamos por el numerador.
24/12 = 2 3 x 2 = 6 Fracción resultante: 6/24
24/8 = 3 10 x 3 = 30 Fracción resultante: 30/24
Y sumamos los denominadores de ambas fracciones, por lo que la fracción que obtenemos de la suma de ambas fracciones es 36/24
Pero esta fracción se puede simplificar si dividimos numerador y denominador entre 12. La fracción irreducible sería 3/2
Aquí puedes ver el tutorial completo de sumar fracciones con el método del mínimo común múltiplo (mcm) y practicar ejercicios online de suma o resta de fracciones.
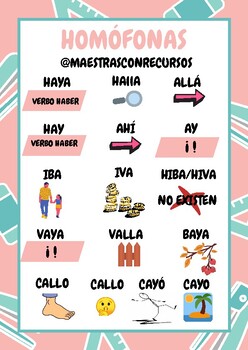
LAS PALABRAS HOMÓFONAS
Las palabras homófonas
Las palabras homófonas son aquellas que se pronuncian de la misma manera, se pueden escribir exactamente igual pero en realidad, pueden tener distinto significado. Para entender mejor las palabras homófonas es importante comprender qué es la homonimia.
La homonimia es la cualidad de dos palabras que tiene distinto origen y significado por evolución histórica, pero que tienen la misma forma (se pronuncian o se escriben igual). Las palabras homónimas tienen unas características que debes conocer:
- Tienen un origen etimológico distinto
- Pueden tener categorías gramaticales diferentes
- Se pueden escribir de forma distinta
- En el diccionario tienen diferentes entradas
Ejemplos de palabras homófonas
- A (primera letra del alfabeto) y Ha (del verbo haber)
- Abollar (realizar abolladuras a un objeto de metal) y Aboyar (colocar boyas en el mar para detener redes o hacer limitaciones)
- Baca (parte superior de un automóvil usada para transportar cosas) y Vaca (animal rumiante)
- Bario (metal de color blanco y plateado) y Vario (diverso)
- Barón (título nobiliario) y Varón (hombre)
- Cabo (extremo, pabilo o grado militar) y Cavo (del verbo cavar)
- Desecha (viene de desechar) y Deshecha (viene de deshacer)
- Sabia (alguien con sabiduría) y Savia (jugo vegetal)
- Sake (bebida alcohólica de arroz hecha en Japón) y Saque (del verbo sacar)
LAS MIL Y UNA NOCHES. ANTOLOGÍA
Todo comienza con un poderoso monarca de la antigua Persia quien tenía dos hijos: Schariar el mayor y Schazenan el menor. Tras la muerte del monarca Schariar sube al trono y su hermano menor quedo reducido a ciudadano. Schazenan no sintió envidia de su hermano, ya que se querían mucho. …
jueves, 26 de noviembre de 2020
miércoles, 25 de noviembre de 2020
DÍA INTERNACIONAL DE LA ELIMINACIÓN DE LA VIOLENCIA CONTRA LA MUJER. 25 NOVIEMBRE
2. Vídeo "Mujeres molonas".
3. Vídeo "¿Sabes lo que es la igualdad de género?
4. Vídeo "Rap en lucha por la igualdad".
5. Spot contra la violencia de género.
6. Anuncio "Ni media broma".
7. Vídeo "Violencia de género - ¿Cuándo se aprende?
8. Rap de El Chojín "Respétate, respétame".
9. Vídeo "Comparte el trabajo doméstico".
* En las siguientes páginas podéis encontrar recursos y dinámicas de todo tipo para trabajar la igualdad de género y la violencia contra la mujer:
10. Adolescentes sin violencia de género.
11. Educar en igualdad.
12. Enrédate sin machismo.
13. Mujeres que cambian el mundo.
domingo, 22 de noviembre de 2020
LAS DESCRIPCIONES
Describir es explicar, de forma detallada y ordenada, cómo son las personas, los lugares o los objetos. La descripción sirve sobre todo para ambientar la acción y crear una atmósfera que haga más creíbles los hechos que se narran. Muchas veces, las descripciones contribuyen a detener la acción y preparar el escenario de los hechos que siguen.